tanx的导数是sec²x（secx的平方）。tanx导数，可把tanx化为sinx/cosx进行推导，(tanx)'=1/cos²x=sec²x=1+tan²x。tanx属于正切函数，是单调递增函数、周期函数、奇函数。
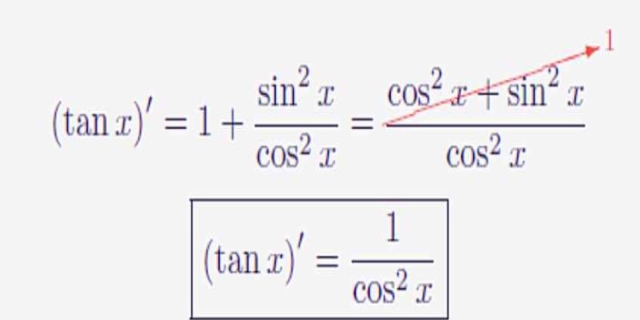
tanx的导数是什么
正切函数的导数，等于对应的余弦函数的平方的倒数(或“正割函数的平方”)，即(tanx)'=1/(cosx)^2(或“(tanx)'=(secx)^2”)。
正切函数(tanx)导数公式的推导过程：
因为“tanx=sinx/cosx”，
所以(tanx)'=(sinx/cosx)'
=[(sinx)'cosx-sinx(cosx)']/(cosx)^2
=[cosxcosx-sinx(-sinx)]/(cosx)^2
=[(cosx)^2+(sinx)^2]/(cosx)^2
=1/(cosx)^2
所以，(tanx)'=1/(cosx)^2。
爬楼梯60-90min相当于慢跑一小时。爬楼梯速度为20-50台阶/min，台阶的高度在14-15厘米，则爬楼梯一小时所消耗热量为480大卡。而慢跑一小时所消耗热量为655大卡，因此爬楼梯60-90min相当于慢跑一小时。爬楼梯多久相当于慢跑一小时爬楼梯可以在室内或室外进行，城镇居民可以利用高楼建筑物内的楼梯进行运动锻炼。上下楼梯一定要把握好节奏，速度不可太快，避免跌倒。慢跑是一种中等强度的有氧运
柳条像什么比喻句：柳条像优雅的舞者，轻轻摇曳着身姿。柳条如绿色的丝带，在微风中飘动。柳条似少女的长发，柔美又飘逸。柳条就像是大自然的画笔，在春风中描绘出生机勃勃的画卷。柳条像什么比喻句柳条犹如绿色的琴弦，在风中弹奏出自然的旋律。柳条仿佛绿色的瀑布，从树梢倾泻而下。柳条就像细长的绿箭，指向春天的方向。柳条如同绿色的流苏，装饰着春天的树梢。柳条似轻盈的燕子，在风中自由飞翔。柳条就像绿色的波浪，在微风中
小升初看语文、数学和英语。语文、数学和英语作为三门主科，其成绩往往是小升初时最被看重的。这些科目不仅考查了孩子们的基础知识掌握情况，还体现了他们的思维能力、分析能力和问题解决能力。因此，孩子们在这些科目上的表现往往会被作为评估他们学习能力的重要指标。小升初看什么成绩其次，除了基础学科成绩外，孩子们的综合素质也是小升初时不可忽视的方面。这包括他们的学习习惯、学习方法、团队协作能力、创新能力等多个方面
“我丢”是一个在日常口语中经常出现的表达，尤其在中国的南方地区，例如广东、福建等地，人们经常使用这个词组来表达惊讶、不满、疑惑等情绪。这个词组的字面意思是“我丢失了”或“我失去了”，但在实际使用中，它更多地被用作一种语气感叹词，而非真的表示丢失了某样东西。我丢是什么意思从字面上来看，“我丢”意味着某样东西的丧失。在日常生活中，当我们真的丢失了钥匙、手机等物品时，可能会脱口而出“我丢！”来表示自己的
孱头是一个汉语词语，通常用来形容那些软弱无能、胆小怕事的人。这个词源于古代汉语，其中“孱”指的是软弱、怯懦，而“头”则代表人的身份或地位。因此，“孱头”就是用来形容那些缺乏勇气、决心和坚定立场的人。孱头的意思在日常生活中，我们可能会遇到各种各样的人，有些人在面对困难和挑战时能够坚定立场、勇往直前，而有些人则会因为害怕失败或承担责任而犹豫不决、退缩不前。这些人往往被形容为“孱头”。除了形容人的性格特
作揖的正确姿势：双脚并拢，身体挺直，肩膀放松，目视前方。这种站姿给人一种庄重而自信的感觉，为接下来的作揖动作打下了良好的基础。双手合十。将右手掌心向内，置于左手掌之上，两拇指轻轻相接，形成一个微微向上的弧形。这个手势象征着和谐与团结，也体现了对对方的尊重。作揖的正确姿势接下来，开始作揖。身体微微前倾，双手从胸前开始，随着身体的前倾，缓缓推出。推出时，双手保持合十的姿势，高度略低于胸部，然后双手停止
激励理论用途：提高工作效率：激励理论可以帮助管理者了解员工的需求和动机，从而设计出更有效的激励机制。通过满足员工的需求，激发其内在动力，可以提高员工的工作效率和创造力，进而提升整个组织的绩效。激励理论有什么用增强团队凝聚力：激励理论强调个体与组织目标的一致性，通过合理的激励机制，可以使团队成员更加团结，形成共同的价值观和目标追求。这有助于增强团队的凝聚力和向心力，使团队在面对挑战时更加团结一致。促
睡眠模式1（通用睡眠模式）适合大多数消费者，因为它能够根据环境温度自动调节，提供舒适的睡眠环境。睡眠模式2适用老年人、妇女等消费者，或者睡觉时着装很少的用户，因为它能够适度调温。睡眠模式3则适用中青年消费者，因为它可以湿度调温，并且在睡眠模式结束前温度将自动调回来。睡眠模式4则是专门为儿童设计的，因为它能够保持室内温度相对稳定。睡眠1234哪个适合晚上睡觉睡眠模式2是按照设定的一组睡眠曲线进行运行
7一12岁手工废物利用：1. 纸盒小房子材料：废旧纸盒、剪刀、胶水、彩纸、颜料等。步骤：孩子们可以将纸盒切割成合适的形状，用胶水粘贴成一个小房子的结构。再用彩纸和颜料进行装饰，一个精美的小房子就完成了。7一12岁手工废物利用2. 塑料瓶花盆材料：废旧塑料瓶、土壤、种子、彩带等。步骤：孩子们可以在塑料瓶上打孔，填充土壤并种上植物。用彩带或其他材料装饰塑料瓶，使其成为既实用又美观的花盆。3. 旧衣物改
拉丁美洲共有34个国家及若干未独立地区，这些国家包括墨西哥、危地马拉、洪都拉斯、萨尔瓦多、尼加拉瓜、哥斯达黎加、巴拿马、古巴、海地、多米尼加、牙买加、特立尼达和多巴哥、巴巴多斯、格林纳达、多米尼加联邦、圣卢西亚、圣文森特和格林纳丁斯、巴哈马、圭亚那、法属圭亚那、苏里南、委内瑞拉、哥伦比亚、巴西、厄瓜多尔、秘鲁、圣基茨和尼维斯、玻利维亚、智利、阿根廷、巴拉圭、乌拉圭、伯利兹、安提瓜和巴布达。拉丁美洲
最好听的十大铃音包括《Something Just Like This》《红昭愿》《i am you》《起风了》《Dream It Possible》《wonderful u》《纸短情长》《说散就散》《空空如也》和《刚好遇见你》。最好听的十大铃音治愈系音乐：轻柔的钢琴曲、小提琴曲等治愈系音乐，能够抚平人们的烦躁情绪，带来宁静和放松。这类铃音适合在工作或学习压力大的时候使用。动漫游戏音乐：很多动漫和
工龄39年意味着某人在某个单位或行业工作了39个年头，而40年则意味着整整四十年的辛勤付出。虽然只相差一年，但在一些国家和地区，这一年的差距可能会带来实质性的利益差别。工龄39年和40年的区别在很多国家的退休制度中，工龄是一个重要的考量因素。例如，某些地方规定，工龄达到一定年限的员工可以享受全额退休金或其他福利。而这一年之差，可能就意味着某人是否能够达到这一标准，从而享受到相应的待遇。此外，工龄的
苏U是江苏省苏州市。苏州市，这座拥有深厚历史文化底蕴和繁荣现代经济的城市，是长江三角洲关键的中心城市之一。它位于江苏省东南部地区，太湖之滨，长江南岸的人海处处，优越的地理位置，交通要冲便捷。苏u是江苏什么城市苏州的历史可以追溯到公元514年，吴王阖闾命伍子胥建城，距今已有2500年的历史。作为吴文化的发祥地，苏州有着丰富的文化遗产和自然景观。古典园林、古镇水乡、寺庙古刹、名人故居等众多旅游资源，让
“marry”是一个动词，通常用于表达两个人之间的婚姻关系。例如，当两个人决定要结婚时，可以说：“They decided to marry each other.”（他们决定要结婚。）在这个句子中，“marry”表达了两个人之间将要建立的婚姻关系。marry的用法从时态和语态上来看，“marry”有多种时态和语态形式。例如，现在时形式是“marry”，过去时形式是“married”，进行时形式是
“报得三春晖”出自唐代诗人孟郊的《游子吟》。全诗根据描绘1个看似寻常的临走之前缝衣的画面，突显并歌颂了母亲的伟大与无私奉献，表达了作者对母爱的感激以及对于母亲深沉的爱与尊敬。报得三春晖是什么意思“谁言寸草心，报得三春晖”这两句诗采用传统的比兴手法，将儿女比作小草，而母爱则如同春天的阳光，普照并滋养着小草。小草微弱的孝心，无论如何也报答不了春天阳光那般的慈母恩情。这里的“寸草心”指的是子女对母亲的孝
回合制手游是一类游戏玩法，指的是多个玩家按照一定规则顺序操作和控制游戏元素的游戏形式。回合制游戏最早源自于早期的欧洲桌面战棋游戏，其中比较有名的是《龙与地下城》系类。回合制游戏是一类策略游戏，而且是最早推广联网功能的游戏之一。回合游戏手游是什么回合制游戏是一场游戏打怪方式，全部游戏内玩家轮着自己的回合，只有等到自己的回合，才可以进行操纵。比较常见的回合制手游有《梦幻西游》《梦幻诛仙》《修仙物语》等
1008611查询话费余额不收费。1008611是中国移动推出的专门用于查询话费、流量信息的电话，客户拨打归属地1008611后随即挂机，接着会收到话费信息短信，实现了随时便捷查询。1008611查询话费余额收费吗1008611是中国移动为了方便客户查询话费、流量等信息而设立的一个自助服务热线。它提供了24小时的服务，客户可以在任何时间进行查询和办理业务。客户拨打归属地1008611后随即挂机，接
“hundred”是一个英文单词，它的发音可以拆分为两个音节：“hun-”和“-dred”。“hun-”部分：发音时，将舌头放在口腔的中央或稍微向后，但不要接触到喉咙。“hun”这个音节的发音与汉字“魂”的发音相近，但请注意英语中的“h”是无声的，所以不需要像发汉语“h”那样用力送气。这个音节的重点是元音“u”，要确保这个元音清晰而饱满。hundred怎么读“-dred”部分：“dred”的发音可
火车硬座，作为铁路交通中最为基础的座位类型，长久以来承载着亿万旅客的出行记忆。它不仅是一种交通工具的座位，更是中国铁路文化的象征之一。下面，我们将从多个方面来详细探讨火车硬座的特点与体验。火车硬座怎么样火车硬座的设计通常简单实用，没有过多的奢华装饰。座位通常由硬质的塑料或木质材料制成，表面覆盖一层薄薄的垫子，虽然不够柔软，但足以应对短途旅行的需求。座位之间的空间有限，旅客需要保持相对紧凑的坐姿，这
摘要怎么写论文：简洁明了：摘要应该简短明了，一般不超过论文全文的5%至10%。因此，需要精选论文中的关键信息，避免冗长和繁琐的表述。摘要怎么写论文概括主要内容：摘要应该概括论文的主要研究内容，包括研究背景、研究目的、研究方法、研究结果和结论等。这些内容应该按照逻辑顺序排列，让读者能够快速了解论文的核心内容。突出研究亮点：摘要应该突出论文的研究亮点和创新点，即论文最为重要的、最具创新性的内容和结论。
